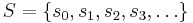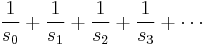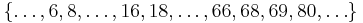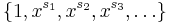Small set (combinatorics)

For other uses of the term, see Small set (disambiguation).

In combinatorial mathematics, a small set of positive integers

$S = \{s_0,s_1,s_2,s_3,\dots\}$

is one such that the infinite sum

$\frac{1}{s_0}%2B\frac{1}{s_1}%2B\frac{1}{s_2}%2B\frac{1}{s_3}%2B\cdots$

converges. A large set is any other set of positive integers (i.e. one whose sum diverges).

1 Examples
2 Properties
3 Open problems
4 Notes
5 References

Examples

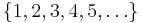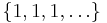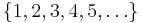The set $\{1,2,3,4,5,\dots\}$ of all positive integers is known to be a large set (see Harmonic series), and so is the set obtained from any arithmetic sequence (i.e. of the form an + b with a ≥ 0, b ≥ 1 and n = 0, 1, 2, 3, ...) where a = 0, b = 1 give the multiset $\{1,1,1,\dots\}$ and a = 1, b = 1 give $\{1,2,3,4,5,\dots\}$ .

The set of square numbers is small (see Basel problem). So is the set of cube numbers, the set of 4th powers, and so on... And so is the set of any polynomial numbers of degree k ≥ 2 (i.e. of the form $a_k n^k%2Ba_{k-1} n^{k-1}%2B\cdots%2Ba_2 n^2%2Ba_1 n^1%2Ba_0$ , with a ≥ 1, a_i ≥ 0 for all i ≥ 1 but a_i > 0 for at least one i ≥ 2, and n = 0, 1, 2, 3, ...). Polynomial numbers of degree k < 2 give an arithmetic sequence (which form a large set.) Polynomial numbers of degree 2 give a quadratic sequence which form a small set. Polynomial numbers of degree 3 give a cubic sequence which also form a small set. And so on...

The set 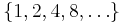$\{1,2,4,8,\dots\}$ of powers of 2 is known to be a small set, and so is the set of any geometric sequence (i.e. of the form abⁿ with a ≥ 1, b ≥ 2 and n = 0, 1, 2, 3, ...).

The set of prime numbers has been proven to be large. The set of twin primes has been proven to be small (see Brun's constant). A property of prime powers used frequently in analytic number theory is that the set of prime powers which are not prime (i.e. all pⁿ with n ≥ 2) is a small set although the primes are a large set.

The set of perfect powers is small.

The set of numbers whose decimal representations exclude 7 (or any digit one prefers) is small. That is, for example, the set

$\{\dots, 6, 8, \dots, 16, 18, \dots, 66, 68, 69, 80, \dots \}$

is small. (This has been generalized to other bases as well.) See Kempner series.

Properties

A union of finitely many small sets is small, as the sum of two convergent series is a convergent series. A union of infinitely many small sets is either a small set (e.g. the sets of p², p³, p⁴, ... where p is prime) or a large set (e.g. the sets 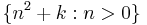$\{n^2 %2B k�: n > 0 \}$ for k > 0). Also, a large set minus a small set is still large. A large set minus a large set is either a small set (e.g. the set of all prime powers pⁿ with n ≥ 1 minus the set of all primes) or a large set (e.g. the set of all positive integers minus the set of all positive even numbers). In set theoretic terminology, the small sets form an ideal.

The Müntz–Szász theorem is that a set 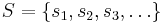$S=\{s_1,s_2,s_3,\dots\}$ is large if and only if the set spanned by

$\{1,x^{s_1},x^{s_2},x^{s_3},\dots\} \,$

is dense in the uniform norm topology of continuous functions on a closed interval. This is a generalization of the Stone–Weierstrass theorem.

Open problems

There are many sets about which it is not known whether they are large or small.

Paul Erdős famously asked the question of whether any set that does not contain arbitrarily long arithmetic progressions must necessarily be small. He offered a prize of $3000 for the solution to this problem, more than for any of his other conjectures, and joked that this prize offer violated the minimum wage law.^[1] This question is still open.

Notes

^ Carl Pomerance, "Paul Erdos, Number Theorist Extraordinaire". Notices of the AMS. January, 1998.

References

A. D. Wadhwa (1975). An interesting subseries of the harmonic series. American Mathematical Monthly 82 (9) 931–933.